The Model is Not the Map
Please Look at the Data
TLDR;
Make maps, not
war(just) benchmarksI made the Santa Fe Quartet as a geospatial equivalent to Anscombe’s quartet
If you are interested in building this kind of map-benchmark let’s chat!
Benchmarks are not enough
In a recent post on on Geospatial Foundation Models, I used publicly available benchmarking data to show that they did not appear to be scaling well. This prompted some healthy discussion around how we should actually measure the utility of some of these models.
I think a fairly obvious answer is: along with model + benchmark releases people should also deploy their model over an actual area and produce a map. This would enable interested users to immediately gauge the quality and the behavior of the model in the wild (aka '“model vibes”). These is just something that looking at the data can tell you that metrics can’t. An additional benefit is: researchers get to feel the pain of practitioners and are more likely to develop models that produce good-looking maps in an operational setting, i.e more useful models. A final hope is that: the community converges towards an easy way to:
take a model
pull input imagery tiles
perform pre-processing
perform inference
stitch the model inference/predictions back together into a map
All preferably for low cost, and fast :).
I should mention that many researchers already do this in the form of Google Earth Engine apps/ ImageCollections, and I think this is absolutely awesome. This definitely makes it infinitely more likely for me to use the model outputs because they are available and easy to overlay with other layers. I would however love to see a DOFA flood map deployed on the Pakistan floods of 2022 that I could overlay with a TerraMind one and a plain U-Net one.
The Santa Fe Quartet
Anscombe’s quartet is one of my favorite datasets: it demonstrates the importance of graphing the data one is analyzing.
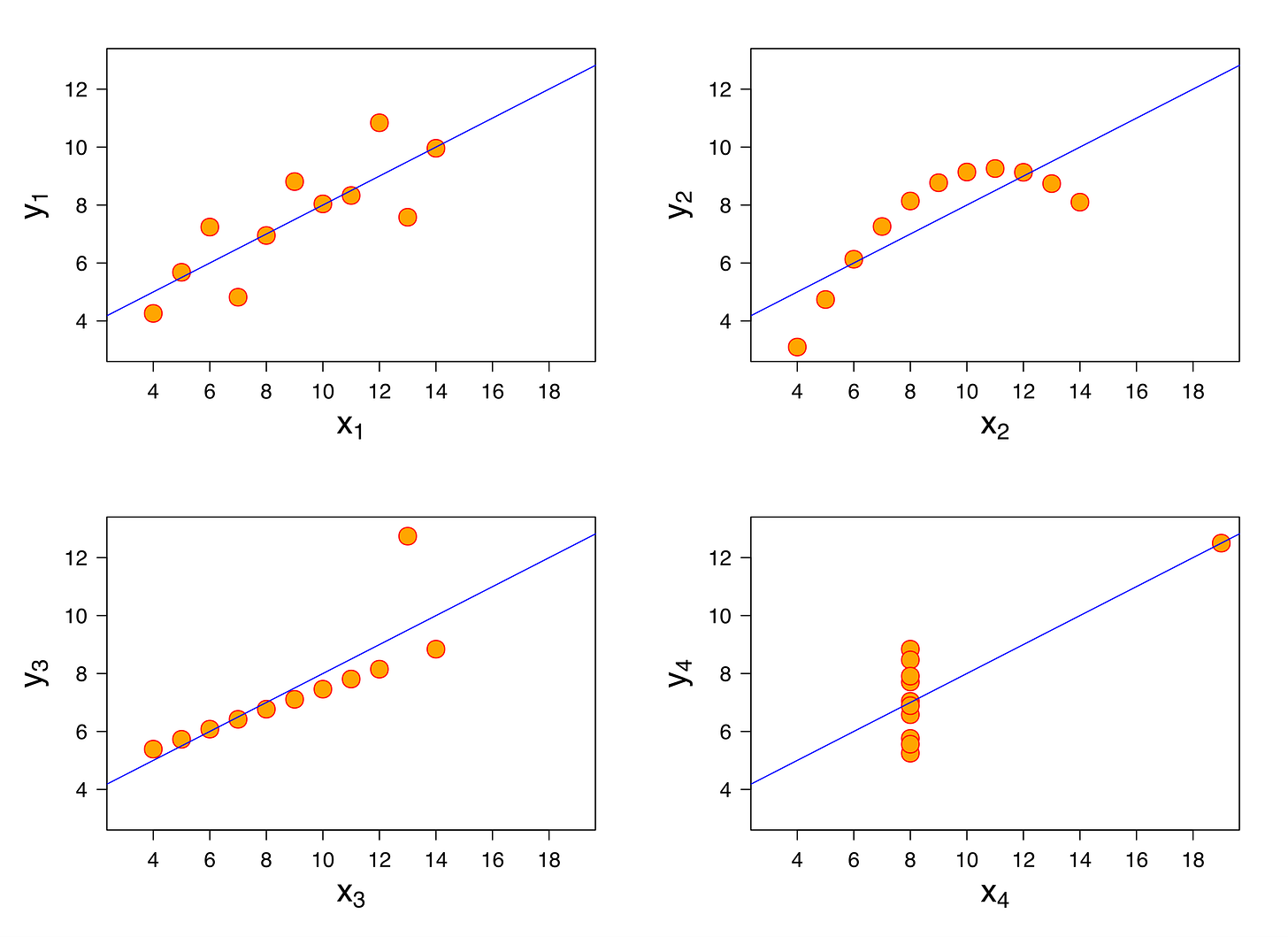
The four datasets depicted below all exhibit the same performance when measured against the linear regression line:

With geospatial data, we have an additional privilege which is that we can also plot our predictions based on their locations on the globe. This allows a variety of different errors to occur, all which tend to be easily addressed and diagnosable if you just look at the map.
To demonstrate this, I pulled a dynamic world tile as an example along with the underlying Sentinel-2 imagery. We’ll simplify this land cover map to just be built area vs non-built area for the purposes of this demonstration. Then we’ll artificially introduce commonly seen geospatial ML map errors, with the constraint that all maps should measure similar f1 score/ intersection1 over union despite the very different underlying processes generating the artificial errors.
In this case we treat the original dynamic world built area map as our ground truth for calculating f1/IoU.


For the first one, I chose areas that were non-built and introduced random ‘salt’ noise. This is a common type of artifact from pixel-wise models.
For the second one I used a binary dilation to expand the existing built area predictions. This can happen if your model is not so hot at classifying edges/boundaries.
In the third I generated artificial tiling artifacts at regular spacing. This can happen if you do not stitch your predictions back properly after tiling.
For the final one, I chose another class from dynamic world (crops), and introduced random salt noise only over that class. This can happen if you have issues in your original training set, i.e not enough differentiation between crops and built-area in this case.
As you can see, all four artificial errors result in f1 scores of ~0.73 and IoUs of ~0.582. If we were to just go by benchmarks, who knows which model we would actually want to use! By looking at actual predictions, especially on a map, we can easily diagnose what major sources of error are and remediate them.
It goes without saying, types of geospatial errors are not limited to these four, and all four can produce different combinations too, but I hope this is illustrative of the need for more than just benchmarks when considering geospatial models, foundational or not!
False positives are much more prominent on a map relative to false negatives, here we focus on introducing those artificially, keeping the false negative rate at 0/constant.
It’s actually a surprisingly complex inverse problem to generate these but also satisfy the constraint of having to have approximately equal f1/IoU. Try it out for yourself!


Great post. A few points I'd make to echo what you wrote, but also to add some nuance from my industry. The first is I like to say that statistics is primarily for understanding data, not, as it's often used, to prove (infer, really) cause and effect. It's about understanding relationships between variables. This, to me, is foundationally important for data science, generally, and I've used Anscombe’s quartet as an example to demonstrate it. There is clearly a better model to be used in some of the cases than simple linear regression, and plotting the data is enough to tell you that (or that there is a problem with the data). Just throwing models at a problem without visually exploring it first can potentially be a waste of time and prone to error. It can also demonstrate when multi-collinearity might be a problem. Quickly plot all your regressors and when you see that many have a correlation with each other and the variable of interest it immediately makes you start to explore what the relationships among variables are with each other, which might be the best, which might have added information, biased, etc. And this sort of visual to explanatory inference is still something that humans do better than machines, if they know enough to do it in the first place.
With that said, my reasoning falls apart with some modern analyses. It's much harder to explore variables when you have hundreds of them. Relationships between variables don't necessarily have to be visibly obvious to humans, and machines can disentangle them, given enough data to do so. The challenge is machine learning approaches are prone to becoming black boxes, so on the whole I still think starting with simpler models and data exploration is the best approach to avoiding overfitting, especially in the case of scenarios where proper cross-validation is not available. This is not uncommon in geology, where datasets are often small, biased, and messy, and where subjective interpretation really needs to play a role. I think the state-of-the-art in geology right now often is overfit models with poor predictive power, especially outside of a small area of interest. And there's a lot more I could write on that, but this reply is already way too long. Maybe it will inspire me to do a follow-up for geology!